あまりしないのですが、line君に頼まれたのでたまにはこういう話もいいかなと。
最小全域木を求める2つのアルゴリズム
最小全域木とは、各辺に非負の重みが付いた無向連結単純グラフの重み最小の全域木です。
クラスカル(kruskal)のアルゴリズム
E(G) を重みが小さい順に整列して、E(G)={e[1],e[2],・・・,e[|E(G)|]} とする
初期化
- V(T):=V(G), E(T):=φ
- S=E(G), i=1 とする
繰り返し
- while (T が非連結)
- begin
- S = S - {e[i]}
- if (T ∪ e[i] が閉路を含まない) E(T) := E(T) ∪ e[i] ;
- i = i + 1;
- end
方針:重みが最小の辺を閉路を含まないように選択していく
プリム(prim)のアルゴリズム
初期化
- V(T):={v}, E(T):=φ, ただし∀v∈V(G).
繰り返し
- while (V(G) - V(T) ≠ φ)
- begin
- V(T) と V(G) - V(T) を結ぶ、重みが最小の辺 e = xy を選ぶ(x∈V(T), y∈V(G)-V(T))
- V(T) := V(T) ∪ {y}
- V(T) := V(T) ∪ {e}
- end
方針:E(T)に隣接する重みが最小の辺を選択していく
例
例として次のようなグラフを考えます。
グラフG
クラスカルのアルゴリズム
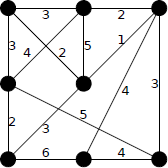
まず重みが1の辺をE(T)に含めます。
次に2も同様に。
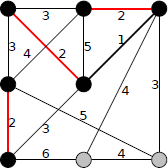
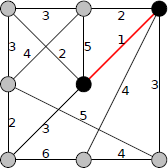
3では、左上の頂点に隣接する辺をE(T)に含めると閉路ができてしまうので含めません。
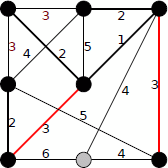
4を含めてTが連結になりました。
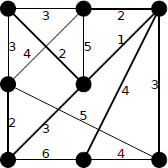
プリムのアルゴリズム
左上の頂点を v(∈V(T)) とします。それに隣接する辺の中で重みが最小の辺は重み2の辺です。
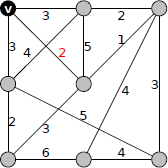
その頂点をTに含めます。そうすると隣接する最小の辺は重み1の辺です。
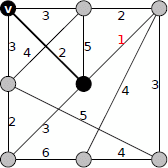
同様に重み2の辺、
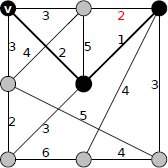
重み3の辺、
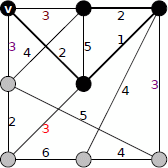
重み2の辺と続きます。
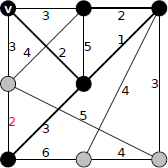
重み3の辺ですが、V(T) と V(G) - V(T) を結ぶ辺は右の辺のみです。
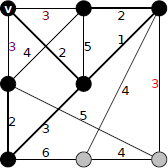
重み4の辺はどちらでもいいです。
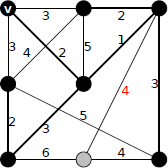
完成
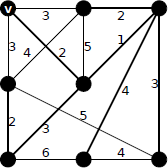
両方のアルゴリズムの結果が同じ形になりましたが、必ずしも同じになるとは限りません(ex.プリムのアルゴリズムの例で最後の重み4の辺の選択をもうひとつの辺にする)
コメントする